授業者　玉置　崇：愛知教育大学附属名古屋中学校教諭　記録者　藤岡　信勝

授業記録（ストップモーション方式による）

１.　問題把握

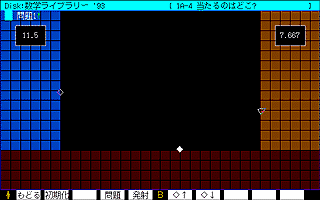
授業開始のチャイムが鳴る。玉置氏は子どもの前に立ってしきりにもみ手をする。高座に上った落語家か漫才師の手つきである。子どもは笑って見ている。 　『これ、先生が緊張しているしるしです』などと言う。これだけでもう教室はいつものリラックスした気分になる。（以下、『』は教師の発言、「」は子どもの発言） 　『まず説明をします』といってホワイト・ボードの前に立ち、タイトル（「当たるのはどこ？」）を東京弁（？）と名古屋弁で言ってみせる。そのつど子どもが笑う。「愛狂亭三楽」の芸名をもつ玉置氏らしい演出である。 　次の手順で説明する。 ホワイト・ボード上にメイン画面が再現されている。磁石（カラー・マグネット）を玉に見立てて動かす。左壁から発射し右壁に当たるようになっていることを示す。左右の壁の上部の窓には高さが数値で出ることを言う。 　 ここまでのことを、コンピュータの画面上でやってみせる。教師用のコンピュータの画面を子どものコンピュータに一斉転送する。[f・6]と[f・7]キーで発射点を上下に動かしてみせる。最初は11.5にして[f・5]キーで発射する。 　 タートルが動き、地面でハネ返って右の壁に衝突して止まる。子どもはこれだけで大喜びである。このときの発射点の高さは11.5、衝突部位の高さは7.667と表示される。

ストップモーション　１ 　本時の条件では、地面の目標物は左から右へ3対2に地面を内分する位置におかれている。したがって比例定数は2／3であるから、右壁に当たった球の位置は72／3、すなわち7.66666･･の循環小数となる。このソフトではそれを小数点以下第4位で四捨五入して7.667と表記した。のちにこの解釈が問題となる。

『今、11.5でやったら7.667になっています。イヤだね、この数字、さてここから問題です。左側の高さが30や1.5の時、「当たるのはどこ？」というのが問題です。（二つの数字を板書する）どうすればいい？』

「やってみればよい」（笑い声） 　『ところが、左側の高さが動くとは言っても、あなたたちが思っているようにはならないんです。あるところまでで制限がつけてあります。そこを、知恵を働かせて、当たるのはどこか見つけて下さい。わかりました？じゃ、君たちの画面に切りかえますから、がんばってやってみて下さい』

（ここまで5分）

２.　個人追求

教室（コンピュータ室）には男女一組につき1台のコンピュータが用意されている。そのペアーごとに課題にとりくむのが個人追求のステップである。 　子どもたちは一斉にコンピュータを操作しはじめた。しかし、アプローチの方向は決して一様ではない。 　まず0.5ずつ入力を変化させて結果を丹念に書きとめているペアーがいる。入力を10,15,20のように整数値で、しかも一定の間隔で動かしているペアーもいる。さらに要領よく、（15：10）（12：8）（18：12）のように整数どうしの対を見つけているペアーもいる。 　また、この先のデータ処理の傾向もさまざまである、整数値の比からいきなり「右が左の2／3になっている」という結論を引き出している子もいれば、丹念に両方の微少増分を調べているペアーもいる。

ストップモーション　２ 　各ペアーには１枚の記録用紙が配布されている。この用紙に、解決までのプロセスをなるべく詳しく記録するよう指示されている。だから、この記録用紙を見るだけで追求がどの方向にどこまで進んだかがおおよそわかる。教師は机間巡視でそれを把握し、次の集団追求のステップにおける指名計画を考えている。

各ペアーにおける男女の分業のあり方は一色ではない。男子がコンピュータを操作し口頭で読み上げ、そのデータを女子が書きとめているという組がやや多いとはいえ、その逆もあり、女子側のイニシアチブで追求が進んでいるペアーも結構多い。理科の実験の授業にしばしば見うけられる男女の積極性の差がほとんど見られないことが印象的である。

（ここまで18分）

３.　集団追求

『はい、それでは、何となく見えてきた人も多いし、あるところで困っている人もいますが、発表し合ってみましょう』 　作業をやめさせておいて言う。 　『まず、答えをきいてみたいと思います。どうやって解いたかは、あとで黒板の前に出て発表してもらいます』 　まず「30」の時の答えをきく。挙手した十数名の中から指名して「20」という答えを得る。「20」になった人を挙手させ得る。ほとんどの子どもが手を上げる。ただし、「20」にならない子もいる。『ならない人は、あとで聞いてみます』といって次に進む。 　同様にして「1.5」の時「1」になるという答えを得る。これは満場一致。 　『それでは、「30→20」について、いろんなやり方をしていた人がいたので、指名させてもらう。前に出て、簡単でいいから書いて説明して下さい。』 　Y君、Kさん、Nさん、そして、「20」にならなかったSさんのペアーが指名される。ホワイト・ボードにそれぞれ数字を書く。考え方のプロセスをあらわしたものである。書き終わったところで順番に発表させる。

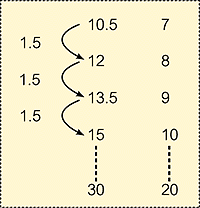Y君の考え（右図は板書） 「最初いろんな数をやってみて、あることに気付きました。1.5増えるごとに当たる壁の方の高さは1ずつふえています。そこから推測して、30の時は20になると思いました」 　『同じ考え方をした人は？』 　8名ほどが挙手する。

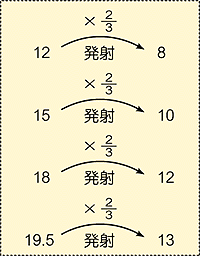Kさんの考え（左図は板書） 「12の時は8、15の時は10、18の時は12、となっていて、発射した壁の高さを当たった壁の高さの関係を図にあらわしてみたら、発射した壁の高さに2／3をかけた高さになっていたから、30×2／3で20としました」 　『そうすると、Y君との考えのちがいは、Y君はタテに（差をとって）比べたのに対し、Kさんはヨコに比較して見ていったということだね』

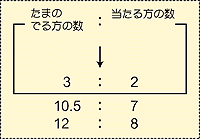Nさんの考え（右図は板書） 「10.5の時は7だからこれは2／3になって、今度は12の時8になったから12÷8、アレッ・・えーと、10.5の時だから7÷10.5で2／3になり、12の時8だから8÷12で2／3。だから玉の当たる方の数は3：2だな、と思って・・・・アレッ・・・・」 　『3：2になってることに気付いたということですね』 　Nさん首をひねりながら席にもどる

ストップモーション　３ 　Nさんは説明の途中で混乱したようだ。この場合、右壁に当たる玉の高さを求める比例定数は2／3だが、左右の比は3：2で、この比の値は3÷2＝3／2（比例定数の逆数）となる。それでNさんは混乱したのだが、正しい推論にもとづく高級なつまづきである。両者のちがいは表現形式上の約束ごとのちがいにすぎないからである。

『さあ、そこで、20にならないよっていう考えがある。これが貴重なんですよね。これちょっとみんなで考えてもらいたいのでは、はい、どうぞ（発表して下さい）』

Sさんの考え（左図は板書） 「はじめ10でやってみたら6.667になって、どんどんやっていったら、0.333、0.333、0.334というふうに増えていった。それから、3増えるごとに2増えるということがわかった。それで20でやった場合、13.333という数字が出て、30まではあと10足りなくなって、3増えるごとに2増えるから、10÷3＝3あまり1で、2×3＝6になって、1余ってるから、上から順に0.333と0.333を足して、それで19.999になった」 　教師はもう一度Sさんの説明をかみくだいて解説した上で、『（この考えに）どう答えますか』と問いかけている。

ストップモーション　４ 　Sさんの考えはユニークで見事な推論である。 データを丹念に分析し、いろいろな観点から増分の対応関係を取り出し、それらをモノサシとして組み合わせて、ぎりぎりのツメをおこなっている。ただし、一か所だけ推論の誤りがある。これは小数点第四位における四捨五入という端数処理に由来する問題なのだが、それを他の子が見ぬけるかどうか。まさにスリリングな場面である。玉置氏にも子どもから正しい反論が出るという確信はなかったそうだ。

Y君が発言する。「これは小数点第三位までしかでなくて、それ以上はないということを考えたら、『約』でいくとY君のように20になるはず」 　Hさんが発言する。「（20から30までの差は）10なんだけど、3で割ると（残り）差は1になって、この場合だと0.5で0.333というふうに増えるわけだけど、順番でいくと、まず0.333ふえて、その次ぎまた0.333ふえて、その次は0.334ふえることになっている。この場合は20の時に13.333だからもうこの時（13に）0.333がプラスされていることになるから、次は＋0.333と＋0.334を足さなきゃいけないけど、Sさんは0.333を二回足しちゃったから0.001足りない。だから、そこ（19.999）に0.001を足せばみんなが言うように20になる。順番になってるから、ちゃんとその数を足せば答えが出る」 「オーッ」という声とともに拍手がわく。

ストップモーション　５ 　この授業の最大のクライマックスである。Y君の指摘は、コンピュータが無限の数値を表示できれば、四捨五入による誤差はなくなるとするもので、この指摘自体は間違ってはいない。しかし、Sさんの推論に用いられた論理を使っていない点で説得力はいま一つである。それに対しHさんは、Sさんがみつけた増分の循環性に目をつけた見事な批判であり、Sさんもこの指摘に百パーセント納得していた。

教師は、ここで左側の高さをx、右側の高さをyとすれば

という関係があること、xとyは「正比例」の関係にあるということを確認する。ここで、「1.5」の時の問題を（a）の式にあてはめて解かせる。 （答えは1）

ストップモーション　６ 　この部分、子どもの動きは必ずしもよくない。 さまざまなアプローチでデータを処理したこの授業のメインの思考作業と(a)式の一般化は異質だからであろう。

『実は先生のコンピュータはどんな数値でも動くようになっているのです』とうれしそうに言い、転送して「30」と「1.5」の場合についてデモンストレーションしてみせる。子どもの出した答えがもちろん正しいことが確認される。 　ついでに「0」の場合をやってみせる。タートルが地面の上を横にすべっていくだけ。笑い声が起こる。

（ここまで43分）

４.　まとめ

『左の高さが40以上で両方の値とも整数になる場合をなるべくたくさんみつけて下さい』 「45と30」「51と34」が出る。 　T君が言う。「9999兆9999億9999万9999と6666兆6666億6666万6666」 　『ごくろうさん。（笑声）でもT君があんなに自信を持ってるのは結局何がわかっているということでしょう』 「2／3かけるっていうことは3で割ることだから割り切れる3の倍数・・・」 　『では最後に2／3は画面のどこにあらわれているだろうか』 　地面の上の目標物の位置が3：2に地面を内分していることを確かめ、次時への発展につなげて終了。

（50分）