体調不良で休みを取られた先生の代役として急遽授業実施。

啓林館2年教科書ｐ124練習１の問題を考える。

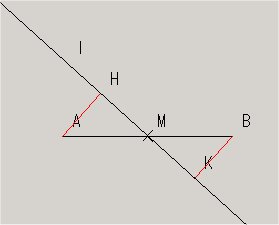
（問題文）線分ＡＢの中点Ｍを通る直線ｌに、線分の両端Ａ，Ｂから、それぞれ、垂線ＡＨ，ＢＫをひきます。このとき、ＡＨ＝ＢＫであることを証明しなさい。

＜初めて教える生徒であることもあって基本の確認から＞
「線分って何ですか」「直線は」という質問から投げかける。はっきり表現できない子どもも多い。「線分には中点があって、直線には中点はあるかどうか」など、おやっと思うような質問を続ける。

問題文を書き、線分と直線との交わる角度について尋ねる。必ずしも教科書の図のようでなくてもいいことを確認。

何を明らかにしなければならないのか、線分が等しいことをいうためにはどんな方法があるかなどを聞き、三角形の合同に目をつける必要性を理解させる。小刻みな確認作業を重ね、証明を終わる。

啓林館2年教科書ｐ１２５問題１を考える。

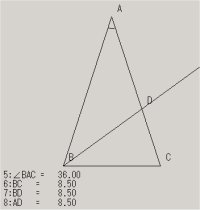
（問題文）頂角∠Ａの大きさが30°の二等辺三角形ＡＢＣがあります。底角∠Ｂの二等分線が辺ＡＣと交わる点をＤとすると、
ＢＣ＝ＢＤ＝ＡＤ　であることを証明しなさい。

前問を生かして、「線分が等しいことを言うのだから、合同を使えばいいね」と揺さぶる。「だめだ」という反応あり。ではどうしたらいいか。二等辺三角形であることを利用するという考えが出る。

二等辺三角形であることを言うために、∠Ａ＝∠ＡＢＤ、∠Ｃ＝∠ＣＢＤであることをいうことに焦点をしぼる。

証明ができたところで、∠Ａが36°でないと成り立たないのかを考える。50°や28°といった意見がでたが、成り立たないことに気づく。36°しか成立しないことを説明して終わる。

啓林館2年教科書ｐ１２５問題２を考える。

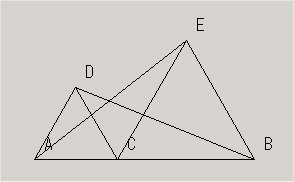
（問題文）線分ＡＢ上に点Ｃをとり、直線ＡＢの同じ側に２つの正三角形△ＡＣＤ、△ＢＣＥをつくるとき、ＡＥ＝ＤＢ　であることを証明しなさい。

問題文には点Ｃの位置はＡＢ上であればいいので、教科書とあえて違う位置に点Ｃをとる。

線分が等しいことを言えという問題→合同は使えるかという問に使えるという反応。では合同である三角形を見つけよという発問。

合同であろうという三角形が見つかったところで、証明に入る。意図的指名により証明を進める。

証明ができたところで、△ＡＣＥがくるっと回ると△ＤＣＢと重なることが分かるかと問う。「回転移動」という発言などにより理解させ終了。